Structural Equation Modeling in R Tutorial 6: Confirmatory Factor Analysis using lavaan in R
Table of Contents
Made for Jonathan Butner’s Structural Equation Modeling Class, Fall 2017, University of Utah. This handout begins by showing how to import a matrix into R. Then, we will overview how to complete a confirmatory factor analysis in R using the lavaan package. Next, I’ll demonstrate how to do basic model comparisons using lavaan objects, which will help to inform decisions related to which model fits your data better. As we go, I’ll demonstrate how to quickly and easily plot the results of your confirmatory factor analysis using semPlot. Last, I’ll demonstrate how to calculate cronbach’s alpha for each of the factors. This syntax imports the 6 variable, 328 person dataset called nep modified.dat, which is a space delimited text file. The data are responses to 6 items, comprising two factors, on the New Ecological Paradigm Scale (NEP:Dunlap et al., 2000), which are survey questions related to attitudes towards the environment, including climate change.
Data Input
First, we will read in the datafile using Fortran and clean up the datafile a little bit, as well as load required packages.
require(lavaan) #for doing the CFA
require(semPlot) #for plotting your CFA
require(psych) #for calculating cronbach's alpha
require(dplyr) #for subsetting data quickly when calculating cronbach's alpha
# make sure to set your working directory to where the file
# is located, e.g. setwd('D:/Downloads/Handout 1 -
# Regression') you can do this in R Studio by going to the
# Session menu - 'Set Working Directory' - To Source File
# Location
cfadat <- read.fortran("nep modified.dat", c("1X", "6F4.0"))
# note that we recode missing values! note: #The format for a
# field is of one of the following forms: rFl.d, rDl.d, rXl,
# rAl, rIl, where l is the number of columns, d is the number
# of decimal places, and r is the number of repeats. F and D
# are numeric formats, A is character, I is integer, and X
# indicates columns to be skipped. The repeat code r and
# decimal place code d are always optional. The length code l
# is required except for X formats when r is present.
cfadat <- read.table("nep modified.dat") #this does the same thing as the read.fortran statement above
# add column names
names(cfadat) <- c("nep1", "nep2", "nep6", "nep7", "nep11", "nep12")
Confirmatory Factor Analysis Using lavaan: Factor variance identification
Since confirmatory factor analysis can be thought of in a structural equation modeling framework, we can implement the lavaan package to test the proposed CFA model below. This can be thought of as both a data reduction technique (reducing number of variables) and a measurement technique (partials out measurement error variance to estimate your construct of interest).
Remember that lavaan defaults to setting the first indicator variable to 1 in order to give the facor a metric. However, in this case we will fix the factor variance of each latent factor at one (as depicted in our model above). This will give the factor a standardized metric (you would interpret it in terms of standard deviation changes (e.g. for every one standard deviation change in factor 1, any variable it predicts increases by Y). Fixing the latent factor variances to 1 is often referred to as a factor variance identification approach.
Remember that * fixes variables to a particular value. The factor 1 and factor 2 variances are fixed to 1 in our code below. Note that if you wanted to to a marker variable identification approach (see later in the handout), you could simply fix the loading of one item in each latent factor to 1, then freely estimate the variances for each latent factor. This would make it so that the latent factor would be in the metric of that item. Note how we must ask lavaan NOT to fix the first indicator in each latent to 1 by using the NA* syntax. If we didn’t do this, lavaan would fix these to 1 in addition to the variances being fixed to 1.
cfa.model <- "F1 =~ NA*nep1 + nep6 + nep11 #make 3 indicator latent F1
F2 =~ NA*nep2 + nep7 + nep12 #make 3 indicator latent F2
F1 ~~ F2 #correlate F1 with F2
F1 ~~ 1*F1 #fix factor variance to 1
F2 ~~ 1*F2 #fix factor variance to 1"
cfa.fit <- cfa(cfa.model, data = cfadat)
summary(cfa.fit, fit.measures = TRUE)
## lavaan 0.6-5 ended normally after 22 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of free parameters 13
##
## Number of observations 328
##
## Model Test User Model:
##
## Test statistic 17.040
## Degrees of freedom 8
## P-value (Chi-square) 0.030
##
## Model Test Baseline Model:
##
## Test statistic 388.208
## Degrees of freedom 15
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.976
## Tucker-Lewis Index (TLI) 0.955
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3013.351
## Loglikelihood unrestricted model (H1) -3004.831
##
## Akaike (AIC) 6052.702
## Bayesian (BIC) 6102.011
## Sample-size adjusted Bayesian (BIC) 6060.776
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.059
## 90 Percent confidence interval - lower 0.018
## 90 Percent confidence interval - upper 0.098
## P-value RMSEA <= 0.05 0.310
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.034
##
## Parameter Estimates:
##
## Information Expected
## Information saturated (h1) model Structured
## Standard errors Standard
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## F1 =~
## nep1 0.959 0.075 12.720 0.000
## nep6 0.569 0.073 7.834 0.000
## nep11 0.998 0.072 13.935 0.000
## F2 =~
## nep2 0.562 0.073 7.685 0.000
## nep7 0.621 0.073 8.473 0.000
## nep12 1.003 0.100 10.054 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## F1 ~~
## F2 0.544 0.065 8.334 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## F1 1.000
## F2 1.000
## .nep1 0.733 0.104 7.055 0.000
## .nep6 1.200 0.101 11.862 0.000
## .nep11 0.470 0.100 4.698 0.000
## .nep2 0.923 0.088 10.469 0.000
## .nep7 0.846 0.088 9.593 0.000
## .nep12 1.110 0.167 6.666 0.000
semPaths(cfa.fit, "par", edge.label.cex = 1.2, fade = FALSE) #plot our CFA
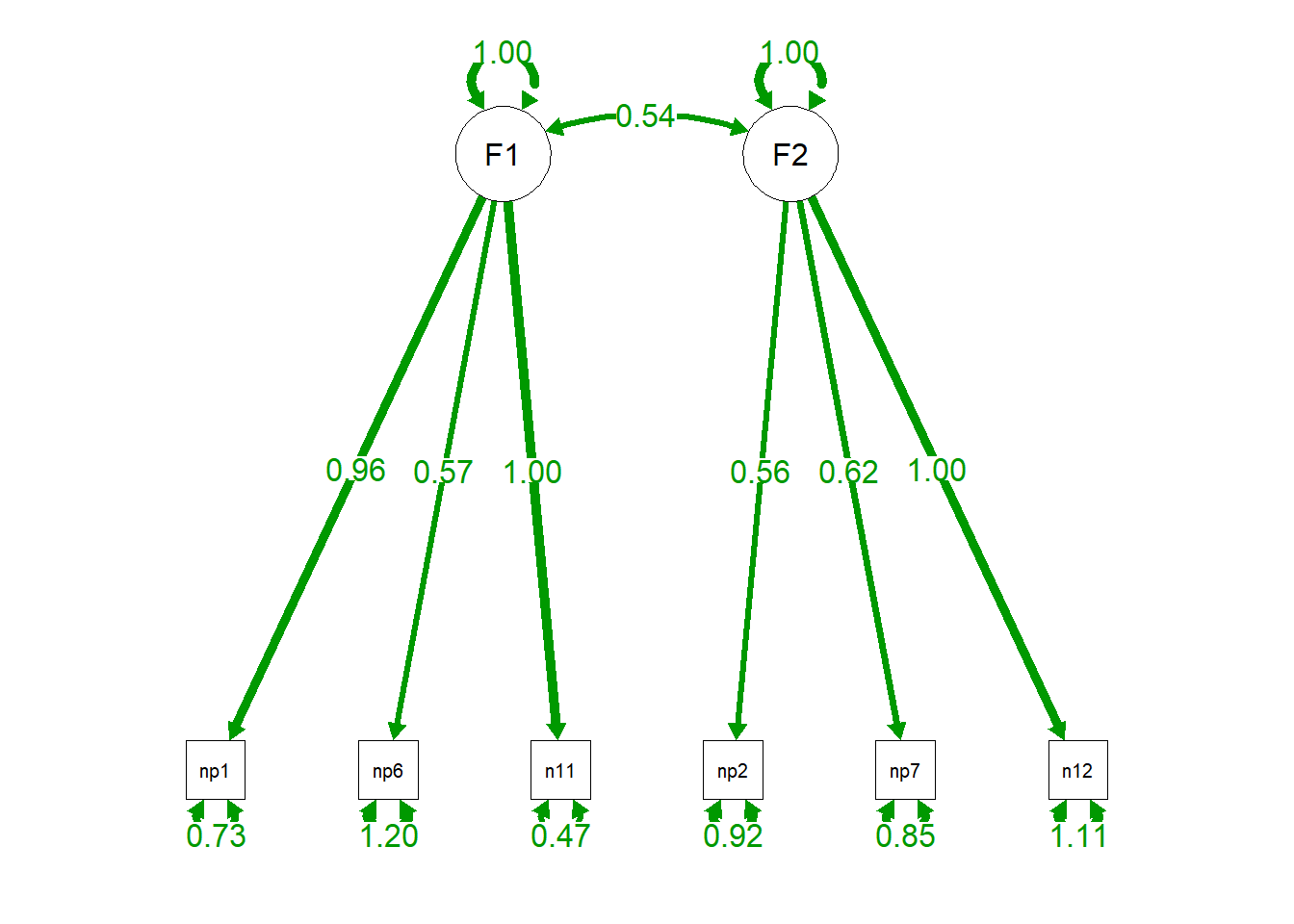Remember that this is the stage where you would be deciding whether items are poor items or not (cross-loadings, where an item loads .4 or above with more than one factor is usually considered poor, or an item that does not load highly with any factor (below .4 or .5) are also generally considered poor (Tabachnick and Fidell, 2011). In this case, you would remove the item and redo the factor analysis.
From this model, we can see that our fit is pretty good (CFI/TLI > .95, RMSEA approaching .05, SRMR < .05). However, we might have reason to believe that factor 1 and 2 do not correlate. Now, we will not estimate an alternative model where we estimate the correlation between factor 1 and factor 2. We have to explicitly specify this in lavaan syntax, since lavaan defaults to estimating all correlations between exogenous (predictor) latent variables. Since we are estimating one less parameter in our model, we gain one degree of freedom and are model is more over-identified. This is going to be important to consider when we compare models.
cfa.model.nocorr <- "F1 =~ NA*nep1 + nep6 + nep11
F2 =~ NA*nep2 + nep7 + nep12
F1 ~~ 0*F2
F1 ~~ 1*F1 #fix factor variance to 1
F2 ~~ 1*F2 #fix factor variance to 1"
cfa.fit.nocorr <- cfa(cfa.model.nocorr, data = cfadat)
summary(cfa.fit.nocorr, fit.measures = TRUE)
## lavaan 0.6-5 ended normally after 22 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of free parameters 12
##
## Number of observations 328
##
## Model Test User Model:
##
## Test statistic 67.347
## Degrees of freedom 9
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 388.208
## Degrees of freedom 15
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.844
## Tucker-Lewis Index (TLI) 0.739
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3038.505
## Loglikelihood unrestricted model (H1) -3004.831
##
## Akaike (AIC) 6101.010
## Bayesian (BIC) 6146.526
## Sample-size adjusted Bayesian (BIC) 6108.462
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.141
## 90 Percent confidence interval - lower 0.110
## 90 Percent confidence interval - upper 0.173
## P-value RMSEA <= 0.05 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.152
##
## Parameter Estimates:
##
## Information Expected
## Information saturated (h1) model Structured
## Standard errors Standard
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## F1 =~
## nep1 0.893 0.085 10.478 0.000
## nep6 0.553 0.074 7.455 0.000
## nep11 1.075 0.088 12.259 0.000
## F2 =~
## nep2 0.543 0.078 6.972 0.000
## nep7 0.641 0.083 7.692 0.000
## nep12 0.999 0.119 8.379 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## F1 ~~
## F2 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## F1 1.000
## F2 1.000
## .nep1 0.856 0.124 6.898 0.000
## .nep6 1.219 0.103 11.801 0.000
## .nep11 0.311 0.154 2.028 0.043
## .nep2 0.944 0.093 10.135 0.000
## .nep7 0.820 0.102 8.044 0.000
## .nep12 1.119 0.211 5.298 0.000
semPaths(cfa.fit.nocorr, "par", edge.label.cex = 1.2, fade = FALSE) #plot our CFA
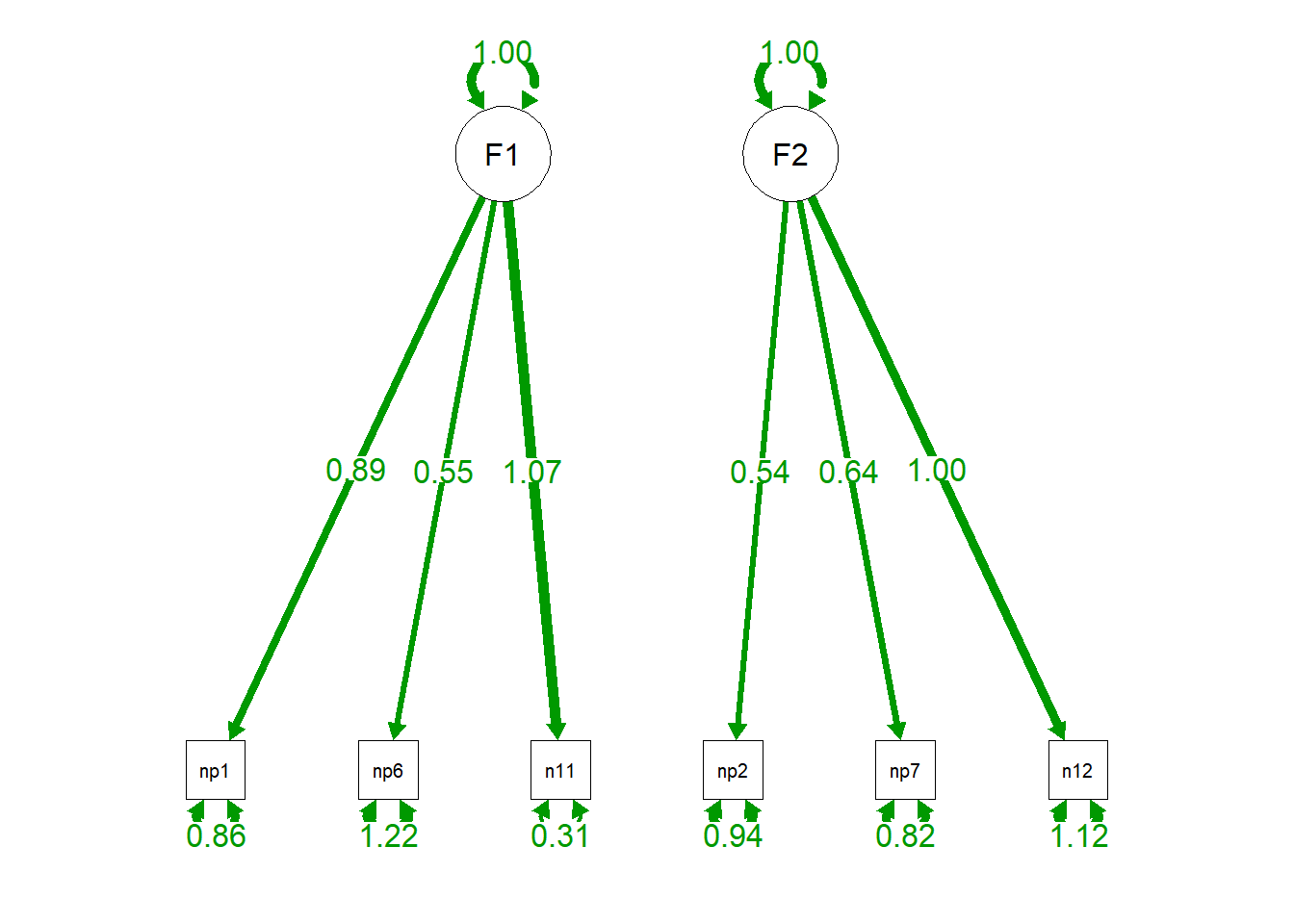
Fit appears to have worsened (CFI/TLI are smaller, RMSEA/SRMR are larger), but we can explicitly test this, which we will do in the next section.
Model Comparison Using lavaan
Note that models that are compared using most fit statistics (with the exception of some, such as AIC/BIC) must be nested in order for the tests to be valid. Nested models are models that contain at least all of the same exact observed variables contained in the less complicated model. The code below compares the reduced model with more df (no correlation between F1 and F2) to the more saturated model with one less df (correlation between F1 and F2 estimated).
anova(cfa.fit, cfa.fit.nocorr) #model fit comparison
## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff
## cfa.fit 8 6052.7 6102.0 17.040
## cfa.fit.nocorr 9 6101.0 6146.5 67.347 50.308 1
## Pr(>Chisq)
## cfa.fit
## cfa.fit.nocorr 0.000000000001314 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Since we reject the null hypothesis using the chi-squared difference of fit test, this means that the more saturated model with the additional parameter estimated (in this case, the correlation between F1 and F2) fits the data better than the more restricted model with that correlation fixed to 0.
###Confirmatory Factor Analysis Using lavaan: Marker variable identification Instead of the factor variance identification approach (latent factor variances fixed to 1), we can adopt what’s referred to as a marker variable identification approach, where we fix the loading of one indicator in each latent to 1 in order to identify the model. This will not change model fit, just some of the loadings in the model.
cfa.model.marker <- "F1 =~ 1*nep1 + nep6 + nep11 #make 3 indicator latent F1 with nep1 as marker
F2 =~ 1*nep2 + nep7 + nep12 #make 3 indicator latent F2 with nep2 as marker
F1 ~~ F2 #correlate F1 with F2"
cfa.fit.marker <- cfa(cfa.model.marker, data = cfadat)
summary(cfa.fit.marker, fit.measures = TRUE)
## lavaan 0.6-5 ended normally after 32 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of free parameters 13
##
## Number of observations 328
##
## Model Test User Model:
##
## Test statistic 17.040
## Degrees of freedom 8
## P-value (Chi-square) 0.030
##
## Model Test Baseline Model:
##
## Test statistic 388.208
## Degrees of freedom 15
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.976
## Tucker-Lewis Index (TLI) 0.955
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3013.351
## Loglikelihood unrestricted model (H1) -3004.831
##
## Akaike (AIC) 6052.702
## Bayesian (BIC) 6102.011
## Sample-size adjusted Bayesian (BIC) 6060.776
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.059
## 90 Percent confidence interval - lower 0.018
## 90 Percent confidence interval - upper 0.098
## P-value RMSEA <= 0.05 0.310
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.034
##
## Parameter Estimates:
##
## Information Expected
## Information saturated (h1) model Structured
## Standard errors Standard
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## F1 =~
## nep1 1.000
## nep6 0.593 0.082 7.242 0.000
## nep11 1.041 0.112 9.298 0.000
## F2 =~
## nep2 1.000
## nep7 1.106 0.187 5.928 0.000
## nep12 1.786 0.296 6.042 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## F1 ~~
## F2 0.293 0.060 4.848 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .nep1 0.733 0.104 7.055 0.000
## .nep6 1.200 0.101 11.862 0.000
## .nep11 0.470 0.100 4.698 0.000
## .nep2 0.923 0.088 10.469 0.000
## .nep7 0.846 0.088 9.593 0.000
## .nep12 1.110 0.167 6.666 0.000
## F1 0.919 0.145 6.360 0.000
## F2 0.315 0.082 3.843 0.000
semPaths(cfa.fit.marker, "par", edge.label.cex = 1.2, fade = FALSE) #plot our CFA
In the figure, you can see the marker variables that we fixed to one. In the output from the model, note how our model fit indices exactly match the model including the correlation when we implemented the factor variance identification approach. The only difference is in the interpretation of the factors, if those factors predict anything else in your model. Here, a one unit change in the factor will correpsonse to a one unit change in the scale/metric of the indicator acting as the marker variable. With questionnaire data for example, it might indicate a one unit change in a likert-style scale.
Calculating Cronbach’s Alpha Using psych
Oftentimes, you’ll want to calculate reliability for each factor once factor structure is established, such as Cronbach’s alpha. Cronbach’s alpha indicates the internal consistency reliability of an item. Mathematically, cronbach’s alpha is the average of all possible split-half correlations between items composing a latent construct. Cronbach’s alpha for each factor can quickly and easily be calculated using the psych package.
# calculate cronbach's alpha...
factor1 <- select(cfadat, nep1, nep6, nep11) #subset data using dplyr
factor2 <- select(cfadat, nep2, nep7, nep12)
alpha(factor1) #function from psych package to calculate cronbach's alpha
##
## Reliability analysis
## Call: alpha(x = factor1)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.7 0.7 0.64 0.44 2.4 0.029 2.9 0.99 0.4
##
## lower alpha upper 95% confidence boundaries
## 0.65 0.7 0.76
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## nep1 0.57 0.57 0.40 0.40 1.3 0.048 NA 0.40
## nep6 0.76 0.76 0.62 0.62 3.2 0.026 NA 0.62
## nep11 0.47 0.47 0.31 0.31 0.9 0.058 NA 0.31
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## nep1 328 0.82 0.81 0.69 0.55 3.1 1.3
## nep6 328 0.72 0.72 0.46 0.39 2.5 1.2
## nep11 328 0.84 0.85 0.76 0.63 3.1 1.2
##
## Non missing response frequency for each item
## 1 2 3 3.5 4 5 miss
## nep1 0.14 0.20 0.21 0 0.30 0.16 0
## nep6 0.26 0.31 0.18 0 0.19 0.06 0
## nep11 0.09 0.30 0.18 0 0.30 0.13 0
alpha(factor2)
##
## Reliability analysis
## Call: alpha(x = factor2)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.6 0.6 0.51 0.34 1.5 0.037 3.4 0.92 0.34
##
## lower alpha upper 95% confidence boundaries
## 0.53 0.6 0.67
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## nep2 0.55 0.57 0.40 0.40 1.32 0.047 NA 0.40
## nep7 0.49 0.50 0.34 0.34 1.01 0.054 NA 0.34
## nep12 0.44 0.44 0.28 0.28 0.79 0.062 NA 0.28
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## nep2 328 0.69 0.72 0.47 0.37 3.1 1.1
## nep7 328 0.72 0.75 0.54 0.42 4.1 1.1
## nep12 328 0.82 0.77 0.59 0.46 3.0 1.5
##
## Non missing response frequency for each item
## 1 2 2.5 3 4 5 miss
## nep2 0.06 0.28 0 0.22 0.35 0.10 0
## nep7 0.03 0.10 0 0.10 0.31 0.45 0
## nep12 0.21 0.22 0 0.12 0.25 0.20 0
A commonly used rule of thumb is that an alpha of 0.7 indicates acceptable reliability and 0.8 or higher indicates good reliability, with .9 or higher being extremely good.
Ian Ruginski
Postdoctoral Fellow
My research interests include spatial cognition, navigation, data visualization, and human-computer interaction.